Spherical Lens

In this article, we are going to study about spherical lens, terms related to them, the nature of image formed, etc.

Table of Contents

• What is Spherical Lens?
• Definitions and Terms related to lens
• Nature and Position of Images formed by Convex lens
• Nature and Position of Images formed by Concave lens
• Lens Formula
• Magnification produced by Lens
• Power of a lens
• Combination of thin lenses in contact

What is Spherical Lens?

Spherical lens is a piece of transparent glass having two curved/spherical surfaces.

Types of Spherical Lens

Spherical Lens are of two types:

• Convex lens (Converging lens)
• Concave lens (Diverging lens)

Note

So, just like we have convex and concave mirrors, we also have convex and concave lens.

Definitions and Terms related to lens

• Principal Axis: It’s the line joining the the centres of curvature of the two bounding surfaces of a lens. Or, we can say that in case of a spherical lens, principal axis is the line joining the optical centre and principal focus.
• Optical Centre (O): It’s a point on the principal axis through which light rays pass undeviated.

Focus and Focal length

When parallel beam of light is incident on a spherical lens, then:

• In case of a convex lens, the refracted rays converge at a point on the principal axis, called Focus (F).
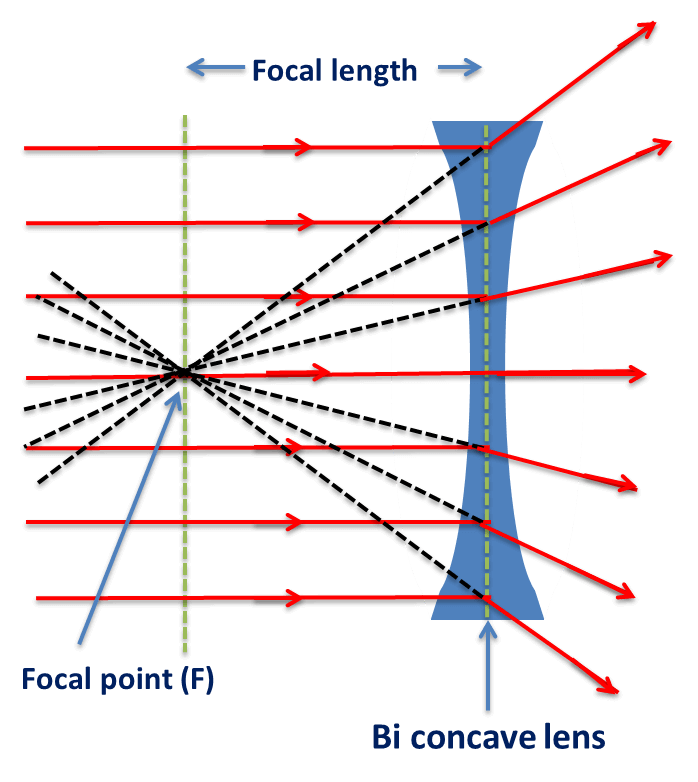
• In case of a concave lens, the refracted rays appear to diverge from a point on the principal axis, called Focus (F).

The linear distance between the Focus (F) and the Optical centre of the lens is called the Focal Length (f) of the lens.

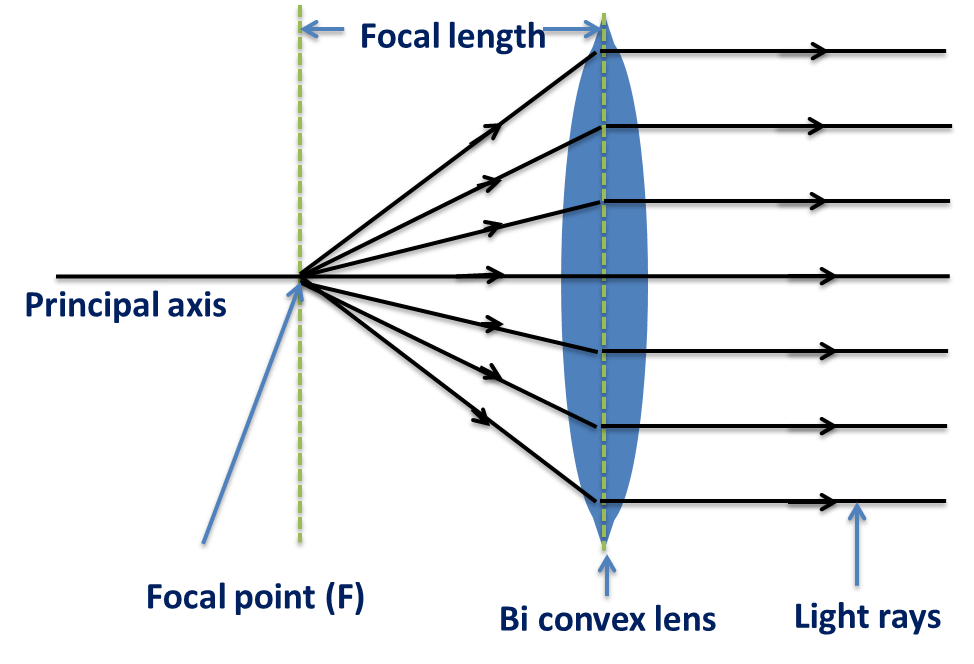
Note

In case of a double convex or concave lens, there are two foci (often written as F and F’, or \(F_1\) and \(F_2\)). The focus on the side of the (original) source of light is called the first focal point, whereas the other is called the second focal point. Both of these focal points are equidistant from the optical centre.

Note

If we split a lens in two equal parts, perpendicular to principal axis, then the focal length of each new lens thus formed is double that of the original lens.

Effect of the medium (in which a lens is kept) on focal length:

• If Refractive index of the medium (in which lens is placed) < Refractive index of the material of the lens, then its focal length increases but nature remains unchanged.
• If Refractive index of the medium (in which lens is placed) > Refractive index of the material of the lens, then the nature of the lens changes.
• If Refractive index of the medium (in which lens is placed) = Refractive index of the material of the lens, then it will work as a plane glass plate.

Nature and Position of Images formed by Convex lens

When an object is placed in front of a convex lens, the position and nature of the image formed will vary based on where the object is placed.

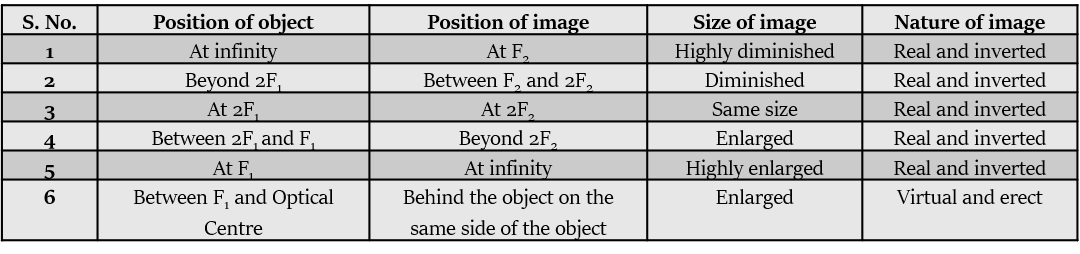
• If the object is at infinity or the incoming rays are parallel to the principal axis, then the image formed by the convex lens will at its second focus (\(F_2\)), i.e. on the right side of the lens. The nature of the image will be - real, inverted and highly diminished.

• If the object is between infinity and 2\(F_1\) (i.e. it’s beyond 2\(F_1\)), the image formed by the convex lens will be between the second focus (\(F_2\)) and 2\(F_2\), i.e. on the right side of the lens. The nature of the image will be - real, inverted and diminished.

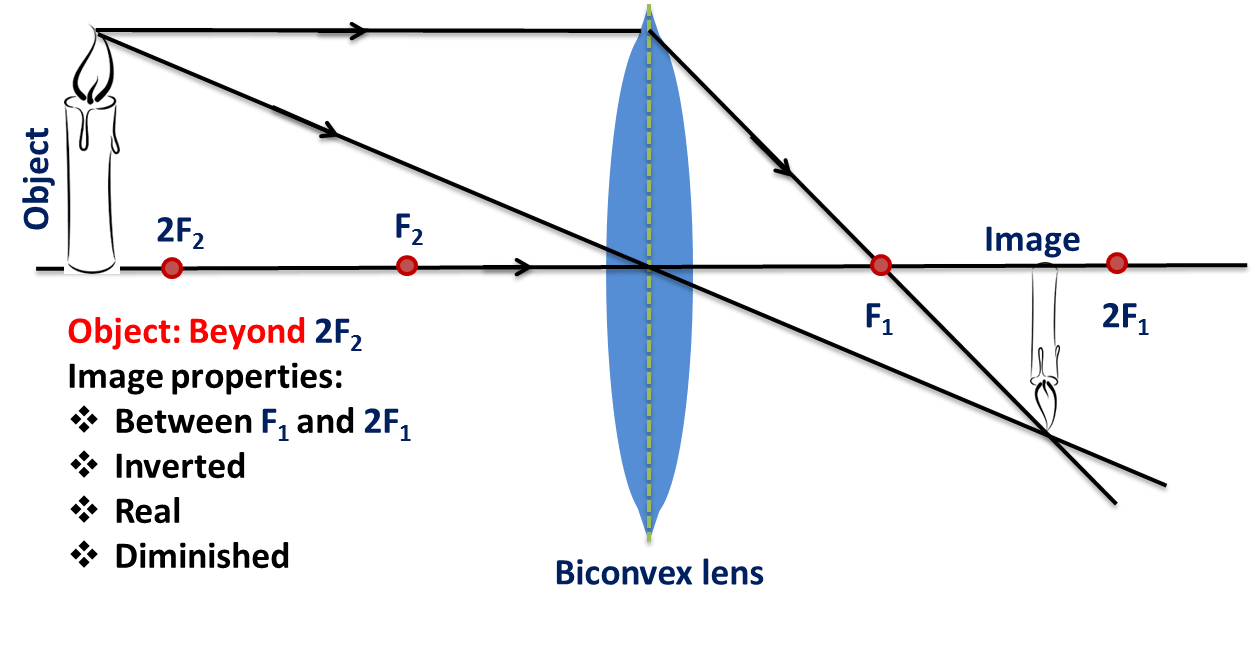
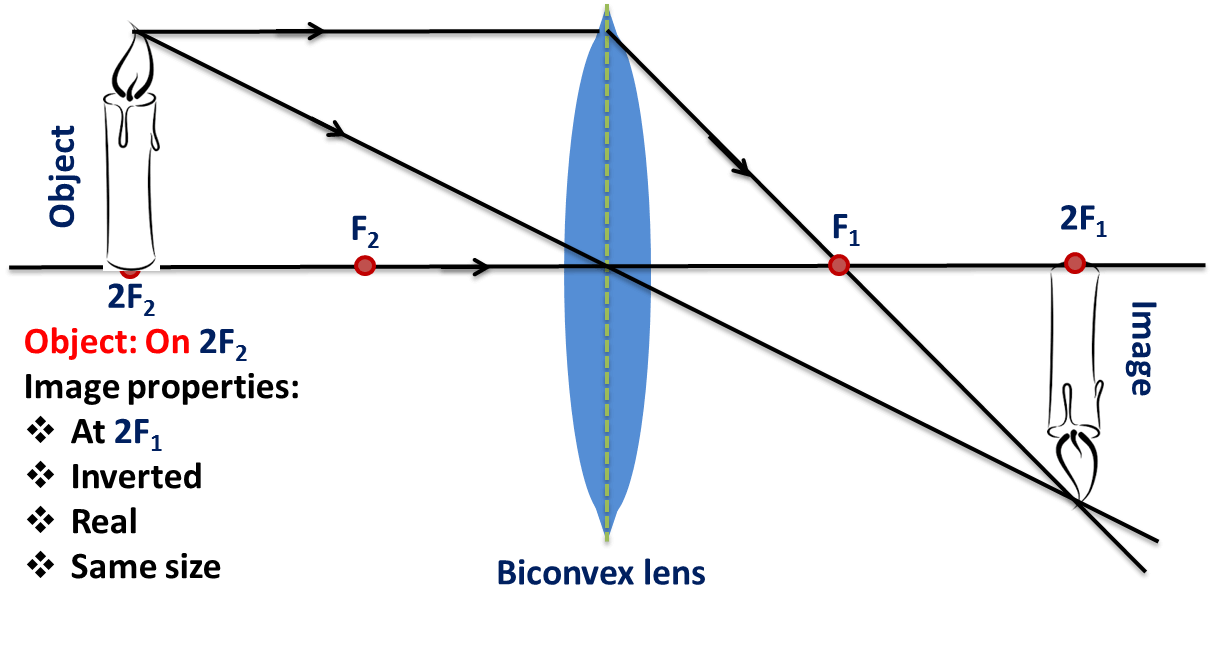
• If the object is at 2\(F_1\), then the image formed by the convex lens will at 2\(F_2\). The nature of the image will be - real, inverted and equal in size as the object.

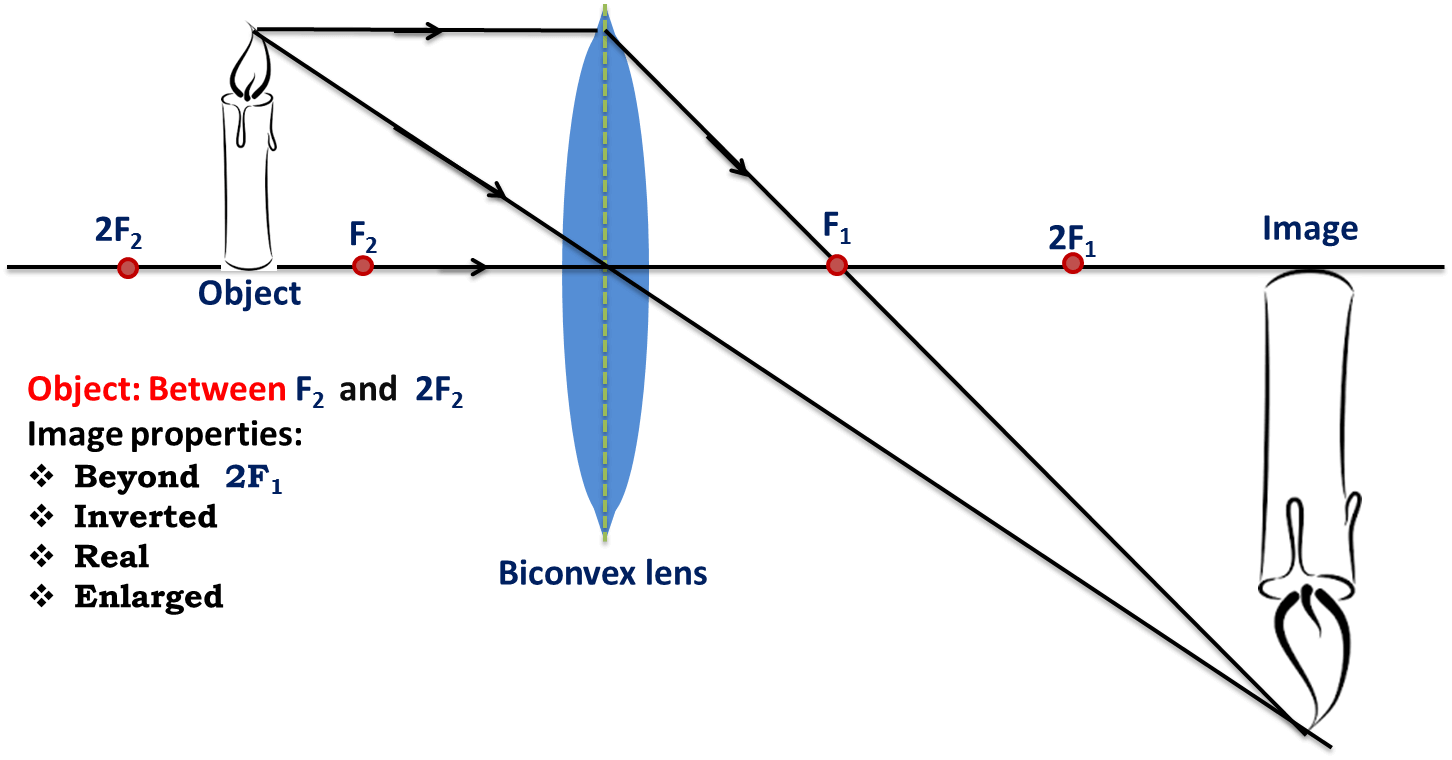
• If the object is between 2\(F_1\) and \(F_1\), the image formed by the convex lens will be beyond 2\(F_2\). The nature of the image will be - real, inverted and magnified (i.e. larger in size than the object).

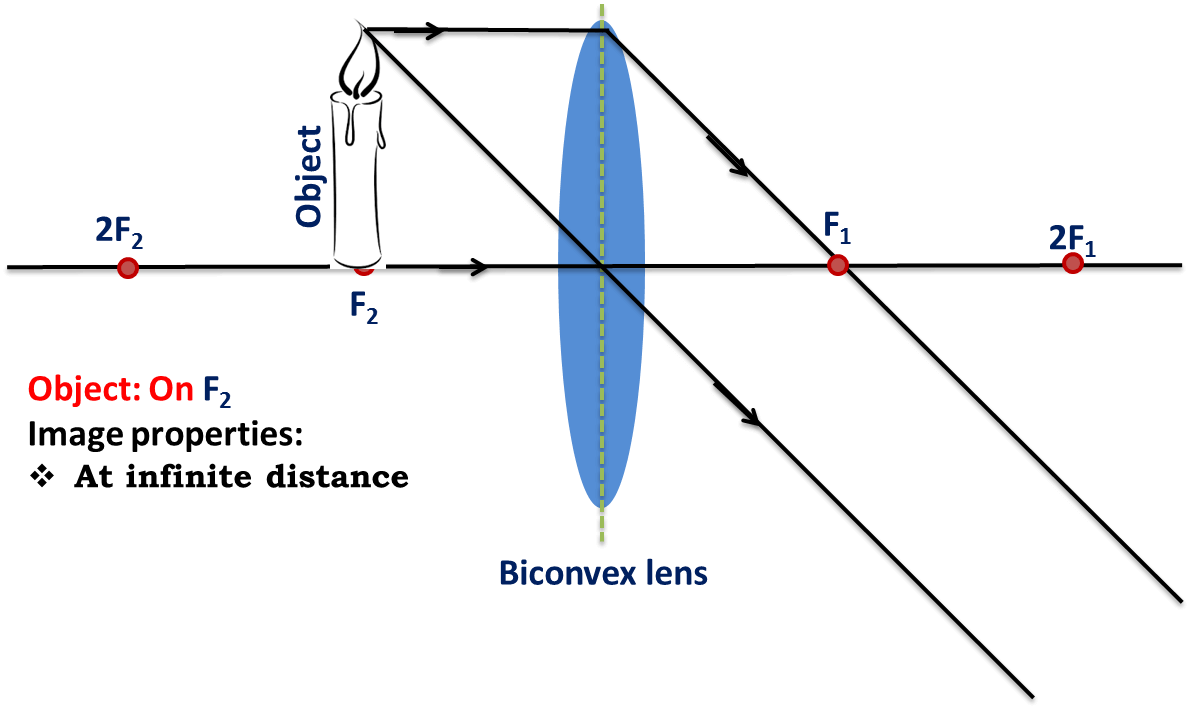
• If the object is at \(F_1\), then the image formed by the convex lens will at infinity. The nature of the image will be - real, inverted, highly enlarged and at infinity.

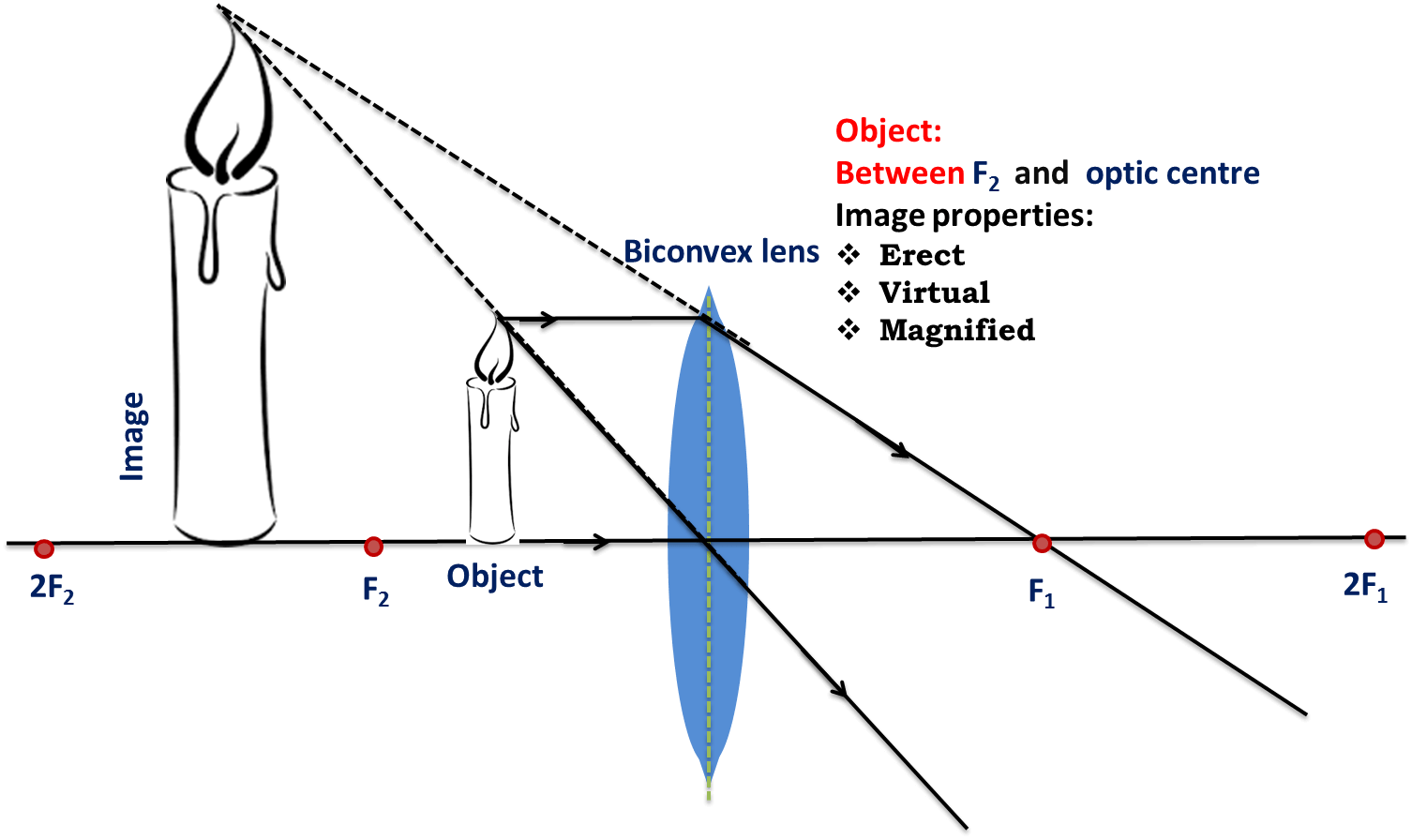
• If the object is between \(F_1\) and Optical Centre (O), the image formed by the convex lens will be behind the object. The nature of the image will be - virtual, erect and enlarged.

It has been summarized in the table given below:

Nature and Position of Images formed by Concave lens

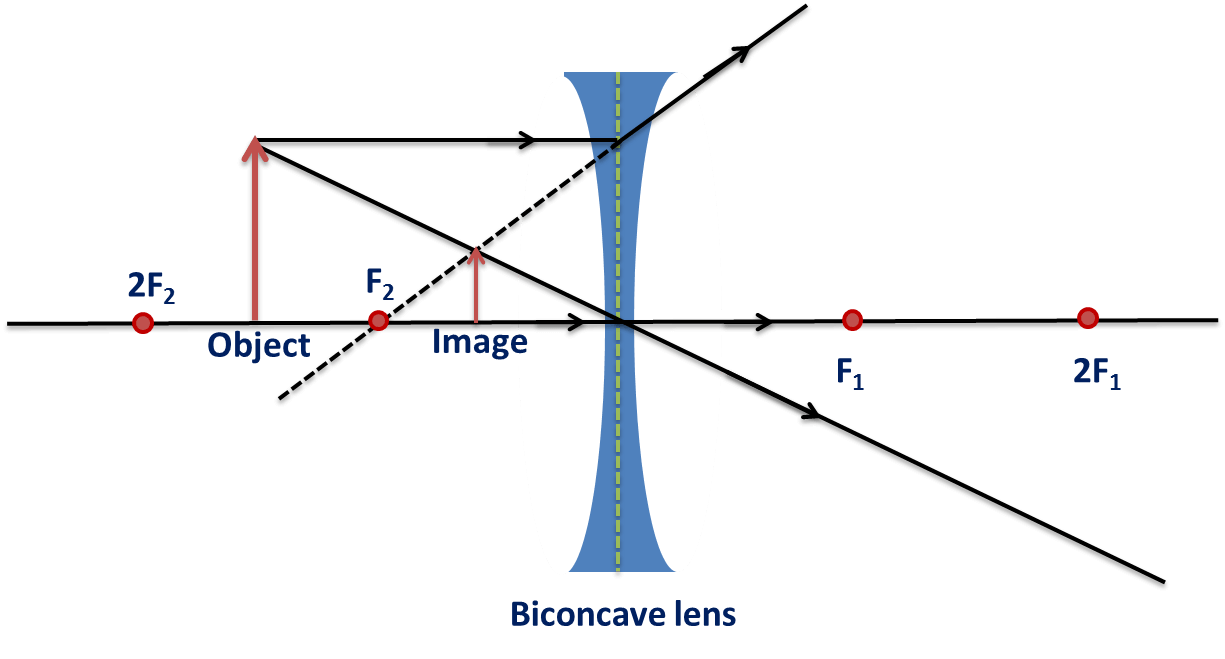
Unlike convex lens, things are much simpler in case of concave lens. Image formed by a concave lens is always virtual, erect and diminished.

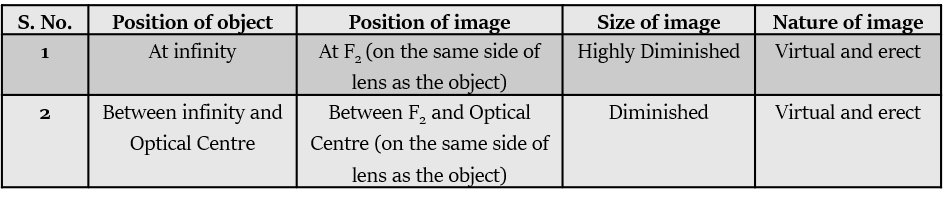
• If the object is at infinity, then the image formed by the concave lens will at \(F_2\). The nature of the image will be - erect, virtual and highly diminished.

• If the object is between infinity and Optical Centre (O), the image formed by the concave lens will be between \(F_2\) and Optical Centre (O). The nature of the image will be - virtual, erect and diminished.

It has been summarized in the table given below:

Lens Formula

Given below is the lens formula that can be applied both in case of convex and concave lens, no matter the image is real or virtual.

\(\frac{1}{f} = \frac{1}{v} - \frac{1}{u}\)

Where, v is the distance of the image from the lens, u is the distance of the object from the lens, and f is the focal length of the lens.

Magnification produced by Lens

Just like in case of mirrors, even in case of lens Magnification (m) is defined as the ratio of the size of the image to that of the object.

That is, Magnification, m = \(\frac{v}{u}\) = \(\frac{Size \hspace{1ex} of \hspace{1ex} image \hspace{1ex} (I)}{Size \hspace{1ex} of \hspace{1ex} object \hspace{1ex} (O)}\)

• Magnification is positive for erect (and virtual) image, whether formed by a convex or concave lens.
• Magnification is negative for inverted (and real) image, whether formed by a convex or concave lens.

Power of a lens

Power of a lens is basically a measure of the convergence or divergence that a lens can introduce on the light falling on it.

Power of a lens is the reciprocal of the focal length of that lens. It is represented by the symbol ‘P’.

That is, P = \(\frac{1}{f}\)

It means that, lens of shorter focal length has more power. Which in turn means that, it bends the incident light more – such convex lens will converge more, while such concave lens will diverge more.

Power of a lens is positive for a convex lens (i.e. converging lens), and negative for a concave lens (i.e. diverging lens).

SI unit of power is dioptre (D). 1D = 1 \(m^{-1}\). The power of a lens of focal length of 1 metre is one dioptre.

Combination of thin lenses in contact

If two or more thin lenses are kept in contact, then:

• Their net power, P = \(P_1 + P_2 + .....\)

• Their effective focal length is given by, \(\frac{1}{f} = \frac{1}{f_1} + \frac{1}{f_2} + .....\)

• Their total magnification, \(m = m_1 × m_2 × .....\)

Combining lens in such a manner helps us to:

• obtain diverging or converging lenses of desired magnification.
• enhance sharpness of the image.

Combination of lenses are often used in cameras, microscopes, telescopes and other optical instruments.

Note

• When lens is dipped in a liquid of higher refractive index, the focal length increases and convex lens behaves as concave lens and vice-versa.

• An air bubble trapped in water or glass appears as convex but behaves as concave lens. Outside water it acts like a convex lens.

• A convex lens of glass when kept inside carbon disulphide appears like a concave lens and vice-versa.